2015年北京市东城区高三上学期期末考试数学（理科）

求二面角 A−PC−B 的余弦值；

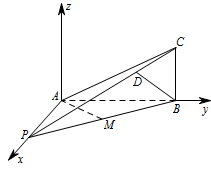
如图，在平面 ABC 内，作 AZ∥BC，则 AP，AB，AZ 两两互相垂直，建立空间直角坐标系 A−xyz．则 A(0,0,0)，P(2,0,0)，B(0,2,0)，C(0,2,1)，M(1,1,0)．

AP−→−=(2,0,0)，AC−→−=(0,2,1)，AM−→−=(1,1,0)．

设平面 APC 的法向量为 n→=(x,y,z)，则

⎧⎩⎨n→⋅AP−→−=0,n→⋅AC−→−=0,

即 {x=0,2y+z=0.

令 y=1，则 z=−2．

所以 n→=(0,1,−2)．

由（1）可知 AM−→−=(1,1,0) 为平面 BPC 的法向量．

设 n→，AM−→− 的夹角为 α，则 cosα=10−−√10．

因为二面角 A−PC−B 为锐角，

所以二面角 A−PC−B 的余弦值为 10−−√10．

⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10分

证明：在线段 PC 上存在点 D，使得 BD⊥AC，并求 PDPC 的值．

答案：

设 D(u,v,w) 是线段 PC 上一点，且 PD−→−=λPC−→−(0⩽λ⩽1)．

即 (u−2,v,w)=λ(−2,2,1)．

所以 u=2−2λ，v=2λ，w=λ．

所以 BD−→−=(2−2λ,2λ−2,λ)．

由 BD−→−⋅AC−→−=0，得 λ=45．

因为 45∈[0,1]，所以在线段 PC 上存在点 D，使得 BD⊥AC．

此时，PDPC=λ=45．

⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14分

已知函数 f(x)=ax−(2a+1)lnx−2x，g(x)=−2alnx−2x，其中 a∈R．

1. 当 a=2 时，求曲线 y=f(x) 在点 (1,f(1)) 处的切线方程；

   答案：

   函数 f(x) 的定义域为 (0,+∞)，f′(x)=(ax−1)(x−2)x2．

   ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分

   当 a=2 时，f′(1)=−1，f(1)=0．

   所以曲线 y=f(x) 在点 (1,f(1)) 处的切线方程为 x+y−1=0．

   ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分

   当 a>0 时，求 f(x) 的单调区间；

   答案：

   f′(x)=(ax−1)(x−2)x2，x∈(0,+∞)．

   1 2 3 4 5 6